ARITMÉTICA BINARIA

Operaciones elementales con números binarios

La Unidad Aritmético Lógica, en la CPU del procesador, es capaz de realizar operaciones aritméticas, con datos numéricos expresados en el sistema binario. Naturalmente, esas operaciones incluyen la adición, la sustracción, el producto y la división. Las operaciones se hacen del mismo modo que en el sistema decimal, pero debido a la sencillez del sistema de numeración, pueden hacerse algunas simplificaciones que facilitan mucho la realización de las operaciones.

                                       Suma en binario

Para aprender a sumar, con cinco o seis años de edad, tuviste que memorizar las 100 combinaciones posibles que pueden darse al sumar dos dígitos decimales. La tabla de sumar, en binario, es mucho más sencilla que en decimal. Sólo hay que recordar cuatro combinaciones posibles:

Las sumas 0 + 0, 0 + 1 y 1 + 0 son evidentes:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

Pero la suma de 1+1, que sabemos que es 2 en el sistema decimal, debe escribirse en binario con dos cifras (10) y, por tanto 1+1 es 0 y se arrastra una unidad, que se suma a la posición siguiente a la izquierda. Veamos algunos ejemplos:

010 + 101 = 111 2₁₀ + 5₁₀ = 7₁₀

001101 + 100101 = 110010 13₁₀ + 37₁₀ = 50₁₀

1011011 + 1011010 = 10110101 91₁₀ + 90₁₀ = 181₁₀

110111011 + 100111011 = 1011110110 443₁₀ + 315₁₀ = 758₁₀

                                             

                                  Sustracción en binario

La técnica de la resta en binario es, nuevamente, igual que la misma operación en el sistema decimal. Pero conviene repasar la operación de restar en decimal para comprender la operación binaria, que es más sencilla. Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia.

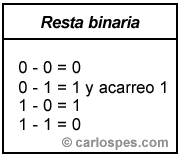
Las restas 0 - 0, 1 - 0 y 1 - 1 son evidentes:

0 – 0 = 0

1 – 0 = 1

1 – 1 = 0

La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 10 - 1, es decir, 2₁₀ – 1₁₀ = 1. Esa unidad prestada debe devolverse, sumándola, a la posición siguiente. Veamos algunos ejemplos:

111 – 101 = 010 7₁₀ – 5₁₀ = 2₁₀

10001 – 01010 = 00111 17₁₀ – 10₁₀ = 7₁₀

11011001 – 10101011 = 00101110 217₁₀ – 171₁₀ = 46₁₀

111101001 – 101101101 = 001111100 489₁₀ – 365₁₀ = 124₁₀

1010111 - 11011 – 10011

A pesar de lo sencillo que es el procedimiento de restar, es facil confundirse. Tenemos interiorizado el sistema decimal y hemos aprendido a restar mecánicamente, sin detenernos a pensar en el significado del arrastre. Para simplificar las restas y reducir la posibilidad de cometer errores hay varias soluciones:

·         Dividir los números largos en grupos. En el siguiente ejemplo, vemos cómo se divide una resta larga en tres restas cortas:

100110011101 1001 1001 1101

010101110010 0101 0111 0010

010000101011 0100 0010 1011

·         Calculando el complemento a dos del sustraendo

     i.        Complemento a dos

El complemento a dos de un número N, compuesto por n bits, se define como:

C_2N = 2ⁿ – N

Veamos un ejemplo: tomemos el número N = 101101₂, que tiene 6 bits, y calculemos su complemento a dos:

N = 45₁₀ n = 6 2⁶ = 64 y, por tanto: C_2N = 64 – 45 = 19 = 010011₂

   ii.        Complemento a uno

El complemento a uno de un número N, compuesto por n bits es, por definición, una unidad menor que el complemento a dos, es decir:

C_1N = C_2N - 1

y, por la misma razón:

C_2N = C_1N + 1

Calculemos el complemento a uno del mismo número del ejemplo anterior:

siendo N = 101101, y su complemento a dos C_2N = 010011

C_1N = C_2N – 1 = 010011 – 000001 = 010010

C_1N = 010010

Da la sensación de que calcular el complemento a uno no es más que una forma elegante de comlicarse la vida, y que no va a ser más sencillo restar utilizando el complemento a dos, porque el procedimiento para calcular el complemento a dos es más difícil y laborioso que la propia resta. Pero es mucho más sencillo de lo que parece.

En realidad, el complemento a uno de un número binario es el número resultante de invertir los UNOS y CEROS de dicho número. Por ejemplo si:

N = 110100101

obtenemos su complemento a uno invirtiendo ceros y unos, con lo que resulta:

C_1N = 001011010

y su complemento a dos es:

C_2N = C_1N + 1 = 001011011

¡es muy fácil!

Veamos otro ejemplo de cálculo de complementos. Sea:

N = 0110110101

El complemento a uno es:

C_1N = 1001001010

y el complemento a dos es:

C_2N = 1001001011

  iii.        Restar en binario usando el complemento a dos

Y, por fin, vamos a ver cómo facilita la resta el complemento. La resta binaria de dos números puede obtenerse sumando al minuendo el complemento a dos del sustraendo. Veamos algunos ejemplos:

Primer ejemplo:

Hagamos la siguiente resta, 91 – 46 = 45, en binario:

1011011 – 0101110 = 0101101

Tiene alguna dificultad, cuando se acumulan los arrastres a la resta siguiente. Pero esta misma resta puede hacerse como una suma, utilizando el complemento a dos del sustraendo:

1011011 + 1010010 = 0101101

En el resultado de la suma nos sobra un bit, que se desborda por la izquierda. Pero, como el número resultante no puede ser más largo que el minuendo, el bit sobrante se desprecia.

Segundo ejemplo:

Hagamos esta otra resta, 219 – 23 = 196, utilizando el complemento a dos:

219₁₀ = 11011011₂, 

23₁₀ = 00010111₂

C₂₂₃ = 11101001

El resultado de la resta será: 11011011 + 11101001 = 111000100

Y, despreciando el bit que se desborda por la izquierda, llegamos al resultado correcto:

11000100₂ = 196₁₀

¡fácil??!

                      Multiplicación binaria

La multiplicación en binario es más fácil que en cualquier otro sistema de numeración. Como los factores de la multiplicación sólo pueden ser CEROS o UNOS, el producto sólo puede ser CERO o UNO. En otras palabras, las tablas de multiplicar del cero y del uno son muy fáciles de aprender:

En un ordenador, sin embargo, la operación de multiplicar se realiza mediante sumas repetidas. Eso crea algunos problemas en la programación porque cada suma de dos UNOS origina un arrastre, que se resuelven contando el número de UNOS y de arrastres en cada columna. Si el número de UNOS es par, la suma es un CERO y si es impar, un UNO. Luego, para determinar los arrastres a la posición superior, se cuentan las parejas de UNOS.

Veamos, por ejemplo, una multiplicación:

Para comprobar que el resultado es correcto, convertimos los factores y el resultado al sistema decimal:

3349 * 13 = 43537

División binaria

Igual que en el producto, la división es muy fácil de realizar, porque no son posibles en el cociente otras cifras que UNOS y CEROS.

Consideremos el siguiente ejemplo, 42 : 6 = 7, en binario:

Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo número de cifras (100 entre 110, en el ejemplo). Si no puede dividirse, se intenta la división tomando un dígito más (1001 entre 100).

Si la división es posible, entonces, el divisor sólo podrá estar contenido una vez en el dividendo, es decir, la primera cifra del cociente es un UNO. En ese caso, el resultado de multiplicar el divisor por 1 es el propio divisor. Restamos las cifras del dividendo del divisor y bajamos la cifra siguiente.

El procedimiento de división continúa del mismo modo que en el sistema decimal.

Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo número de cifras (100 entre 110, en el ejemplo). Si no puede dividirse, se intenta la división tomando un dígito más (1001 entre 100).

Si la división es posible, entonces, el divisor sólo podrá estar contenido una vez en el dividendo, es decir, la primera cifra del cociente es un UNO. En ese caso, el resultado de multiplicar el divisor por 1 es el propio divisor. Restamos las cifras del dividendo del divisor y bajamos la cifra siguiente.

El procedimiento de división continúa del mismo modo que en el sistema decimal.

TIPOS DE COMPUTADORAS

A estos tipos de computadoras se les conocen como microcomputadoras, computadoras personales o computadoras PC ya que están diseñadas para ser utilizadas por una sola persona a la vez. Estas computadoras utilizan un microprocesador como CPU (Central Processing Unit).

Las computadoras PC se usan por lo general en la casa, la escuela o en un negocio. Sus aplicaciones más populares son procesamiento de textos, navegación de internet, correo electrónico, hojas de cálculo, administración de bases de datos, edición de fotografías, creación de gráficos, juegos y música.

Las computadoras personales se encuentran en dos presentaciones, 

computadoras PC de escritorio y computadoras portátiles o laptops.

COMPUTADORAS DE ESCRITORIO

Los tipos de computadoras de escritorio son más grandes, normálmente permanecen en un solo lugar en un escritorio o mesa y se conectan a un tomacorriente. El gabinete puede ser horizontal o tipo torre. Este puede colocarse sobre el escritorio o en el piso.

Estas computadoras cuentan por separado con un Monitor LCD o de tipo CRT, aunque algunos diseños incluyen la pantalla en el gabinete de la computadora. Un teclado y un ratón complementan la computadora para la entrada de datos y comandos.

COMPUTADORAS PORTÁTILES

Los tipos de computadoras portátiles, también llamadas computadoras notebook son pequeñas y lo suficientemente livianas para transportarlas sin problema. Funcionan con baterias, pero también se pueden conectar a un tomacorriente. 

Tipicamente tienen una pantalla LCD interconstruida, la cual se protege al cerrar la computadora para transportarla. También incluyen un teclado y algún tipo de apuntador, tal como una tableta de contacto y un conector para ratón externo.

Aunque algunas laptops son menos poderosas que una computadora de escritorio, este no es siempre el caso. Sin embargo, un computadora portátil cuesta más que una de escritorio con capacidad equivalente. Esto es debido a que los componentes miniatura requeridos para fabricar laptops son mas caros.

PDA's y Computadoras de Mano

Los tipos de computadoras PDA (Personal Digital Assistant) o "palmtop" son microcomputadoras muy pequeñas que sacrifican poder por tamaño y portabilidad. Normalmente utilizan una pantalla de LCD sensible al tacto para la entrada/salida de datos. Las PDA's se pueden comunicar con computadoras portátiles o de escritorio por medio de cables, por rayos infrarojos (IR) o por radio frecuencias. Algunos usos de las PDA's son el manejo de agenda, lista de pendientes, directorios y como cuaderno de notas.

           

Estaciones de Trabajo y Servidores

Los tipos de computadoras conocidos como estaciónes de trabajo son computadoras de alto nivel y contienen uno o más microprocesadores. Pueden ser utilizadas por un solo usuario en aplicaciones que requieren más poder de cómputo que una computadora PC típica, por ejemplo la ejecución de cálculos científicos intensivos o el renderizado de gráficos complejos.

Alternativamente, estas computadoras pueden usarse como servidores de archivos y servidores de impresión a usuarios (Clientes) en una red de computadoras típica. Estos tipos de computadoras también se utilizan para manejar los procesamientos de datos de muchos usuarios simultaneos conectados vía terminales tontas. En este aspecto, las estaciones de trabajo de alto nivel han substituido a las minicomputadoras.

El término "estación de trabajo" tiene otro significado... En una red, cualquier computadora cliente conectada a la red que accesa los recursos del servidor, puede llamarse estación de trabajo. Dicha estación de trabajo puede ser una computadora personal o una verdadera "estación de trabajo" como se definió mas arriba.

Las terminales tontas no se condideran estaciones de trabajo de una red. Las estaciones de trabajo clientes, son capaces de correr programas independientemente del servidor; pero una terminal no es capaz de procesamiento independiente.

Hay otros tipos de computadoras que no son microcomputadoras. Estas se conocen como minicomputadoras, computadoras mainframe y supercomputadoras.

  

                                 Minicomputadoras

Las minicomputadoras son verdaderas computadoras multi-usuario, pero con menos capacidad que las computadoras mainframe. Estos tipos de computadoras aparecieron en los años 1960's cuando los circuitos integrados de grande escala hicieron posible la fabricación de una computadora mucho más barata que las computadoras mainframe existentes. Su costo se redujo en el orden de 10 veces.

Hoy en día, el nicho de las minicomputadoras ha sido ocupado por las estaciones de trabajo de alto nivel, atendiendo a usuarios múltiples.

Computadoras Mainframe

Una computadora mainframe es una computadora grande y poderosa que maneja el procesamiento para muchos usuarios simultaneamente (Hasta varios cientos de usuarios). El nombre mainframe se originó después de que las minicomputadoras aparecieron en los 1960's para distinguir los sistemas grandes de dichas minicomputadoras.

Los usuarios se conectan a la computadora mainframe utilizando terminales que someten sus tareas de procesamiento a la computadora central. Una terminal es un aparato que tiene pantalla y teclado para la entrada / salida, pero que no tiene capacidad de cómputo. También se conocen estas como terminales tontas.

La capacidad de procesamiento de la mainframe se comparte en tiempo entre todos los usuarios. Una computadora PC puede "emular" a una terminal tonta para conectarse a una minicomputadora o a una mainframe. Esto se logra mediante un software especial.

Las computadoras mainframe cuestan varios cientos de miles de dólares. Se usan en situaciones en que las empresas requieren tener centralizados en un lugar tanto el poder de cómputo como el almacenamiento de la información.

Las mainframe también se usan como servidores de alta capacidad para redes con muchas estaciones de trabajo clientes.

Supercomputadoras

Una supercomputadora es una computadora mainframe optimizada en velocidad y capacidad de procesamiento. Las supercomputadoras mas famosas fueron diseñadas por la empresa Cray Inc., fundada por Seymour Cray. La cray-1 se construyó en 1976 y se instaló en el laboratorio Los Alamos National Laboratory.

Estos tipos de computadoras se usan en tareas exigentes de cálculo intensivo, tales como la simulación de la detonación de una bomba atómica, flujos dinámicos y modelos de comportamiento climático global. El costo de una supercomputadora es de varios millones de dólares.

Algunos fabricantes vigentes de supercomputadoras son por ejemplo Cray Inc., Silicon Graphics Inc. y Sun Microsystems.

En tiempos recientes, se han armado algunas supercomputadoras interconectando un gran número de unidades de procesamiento individuales basadas algunas veces en hardware estándar de microcomputadoras.

Todo es Relativo

La afirmación de que algunas computadoras son más poderosas que otras, por ejemplo que las mainframe son más poderosas que las minicomputadoras y que estas a su vez tienen más capacidad que las microcomputadoras, es relativa con respecto al tiempo.

Sin embargo, todos los tipos de computadoras se fabrican cada vez más poderosas con el tiempo y avance de la tecnología. El microprocesador de una computadora de mano es más poderoso de lo que fué la primera y gigantesca computadora ENIAC. Tu computadora PC tiene más capacidad de procesamiento que la primera supercomputadora, etc.

                   Microcomputadoras por Doquier

En la actualidad hay de todos los tipos de computadoras alrededor de nosotros. Los microprocesadores se encuentran en muchos aparatos electrónicos, como tu iPod, tu horno de micro-ondas, en tu automovil, en tu teléfono, etc. Estos aparatos son computadoras de uso especial que corren programas para controlar los equipos y optimizar su desempeño.